Doc Formal: The evolution of formal verification – Part Two
This is the second part of an analysis as to how formal verification has evolved so that it can now be applied to major project challenges. Having described the technology’s foundations in Part One, this article moves on to look at real-world contemporary uses of formal as illustrated by practical examples.
A Practitioner’s View of Formal
The present-day use of formal owes a great deal to the history we considered earlier. Having read that, you will have realized that formal has roots that stretch back for about 70 years and that it comes in different flavors: theorem proving, equivalence checking, and model checking.
There are two ways in which one can become familiar with formal.
The first is to take an even deeper dive into formal’s theoretical foundations that I offered earlier. You will come to understand how formal tools work, what algorithms they use, how the different flavors of theorem provers and equivalence checkers work, or alternatively understand how formal tools are used in practice, and which ones you need to know to get started with formal.
But here I am going to take the second approach. I want to set out formal and its benefits from a user’s point of view, especially with regard to hardware verification. I will focus on the most popular form of formal in use: model checking (alternatively ‘property checking’ or ‘assertion-based verification’). The use of automated apps is not the subject of this article. (The interested reader is referred to this excellent overview by Jim Hogan). I will describe the side of formal that relies on user-defined properties.
Property checking (assertion-based verification)
Property checking or assertion-based verification (ABV) is an automatic method of verifying designs using properties. Though mostly used to verify digital hardware designs, it is also used on analog/mixed-signal (AMS) and SystemC-based designs.
A property captures a specification precisely using notations that have formalized semantics (i.e., a precise unambiguous meaning) and are used to describe the intended behavior of the design-under-test. Well-known property languages include IBM’s Property Specification Language (PSL) and SystemVerilog Assertions (SVA), both of which are derived from their parent language of LTL (invented by Amir Pnueli in 1977).
Let’s look at ABV’s basics using the syntax of SVA, the more widely adopted language. The beauty of languages such as SVA and PSL is that they are synthesizable and can be used in formal verification as well as dynamic simulation. But since a formal model checker enables an exhaustive state-space search, its properties provide a better ROI with a formal tool. This article nicely summarizes where formal ABV outperforms HDL simulation.
SVA (and PSL) come with a rich repertoire for modelling not only Boolean expressions, but also complex temporal expressions. These are called ‘sequences’ and are built by applying temporal operators – such as single cycle implication, next cycle implication, and repetition operators – to model consecutive and non-consecutive repetition, as well as liveness properties.
SVA is built on top of Verilog HDL and consists of three types of properties to capture specifications of the design-under-test (DUT).
1. cover property
This can be true of the DUT sometimes, but is not required to be true always.
2. assert property
This must always be true of the DUT.
3. assume property
This is assumed to be always true of the DUT.
These three forms allow you to capture the time-based (temporal) behavior of the DUT. One important aspect to remember when using properties in SVA is that they are mostly clocked when they are meant to capture time-based behavior. This is so that the model checkers do not have to check (assert or cover) or assume the behavior when the clock is not toggling. This makes model checking very efficient. It is not a requirement that one has to use only a clock; in fact, any event can be used as long as, like a clock, it has an edge—positive (‘posedge’) or negative (‘negedge’). The template for modeling properties then becomes:
[assert|assume|cover] property (@(posedge clock) ...);
The reader should note that use of the word ‘assertions’ in SVA has something of a legacy. Clearly assertions only make up part of SVA; in fact, it is the properties that are the building blocks of the formal layer of SVA. Another facet to point out here is that these properties are synthesizable and can only use the synthesizable subset of Verilog (in the case of SVA) or VHDL (in the case of PSL). This has the advantage that these properties can be used as online monitors in silicon (FPGAs, emulators) and can be used for debugging.
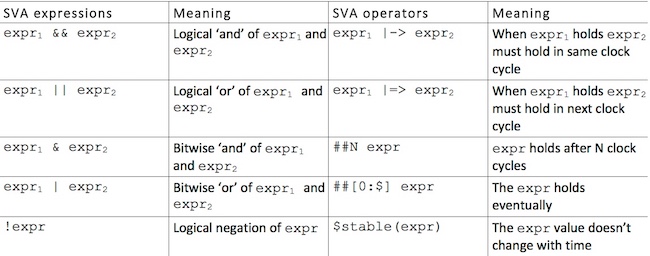
Figure 1 below (adapted from this online article) highlights the most commonly used SVA expressions and operators, distinguishing between the two. Expressions (shown as expr below) are used to build combinational Boolean formulas using standard Verilog Boolean connectives (such as and, or, not), while operators take Boolean expressions and convert them to temporal properties that can express time dependent behavior.
Example 1: A state machine
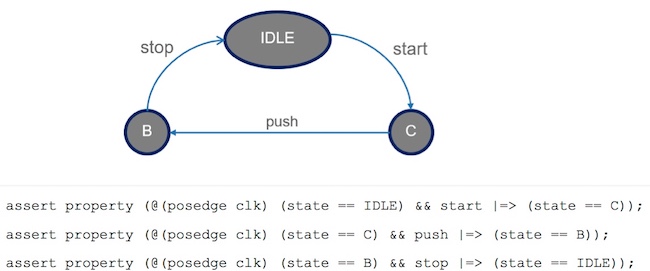
Figure 2 shows a state machine comprising three states: IDLE, B, and C. To specify the behavior of the state machine, we can write three assertions that describe its required behavior. Usually, these state machines are encoded in a hardware description language, such as Verilog or VHDL, and would use a state variable (the state is shown below).
The assertions describe, for example, that if the design is in the IDLE state and a start action is seen, then the next state (following a clock cycle) is C. Similarly, if the state is C and you have a push then the next state is B, and lastly, if the state is B and you have a stop, then the state is restored to IDLE.
Example 2: When to assert and when to assume
The code fragments below illustrate where these two different choices might be made.
assume property (@posedge clk (!(read && write));
A single-port RAM cannot have a read and a write in the same clock cycle.
assert property (@posedge clk (!(empty && full));
A FIFO cannot be empty and full at the same time. This must be a requirement of all FIFOs.
A key point to note here is that a property must only be assumed if it describes a behavior about its environment or uses only inputs of the design. One must not assume a property if it is meant to be a check on the design’s internal state or its outputs. In the above example, we have safely assumed that for a single port random access memory (RAM), in a given clock cycle, one can only do a read or a write, but not both. This behavior must be guaranteed by the driving logic of the RAM’s read and write signals (i.e., its environment). However, for a FIFO, regardless of how it is designed, it must never be true that it is both empty and full: Hence, it is a requirement (check) of the design. This is a subtle but important point about using formal properties: Choosing the correct polarity is one of the most important aspects of formal property checking.
Example 3: When to cover a property
It should be possible that a full FIFO can be eventually drained to empty. Equally, it must be possible to fill up the FIFO from empty. How might this be expressed?
cover property (@posedge clk (empty |-> ##[0:$] full));
cover property (@posedge clk (full |-> ##[0:$] empty));
As it is not a requirement that on every clock cycle a full FIFO must drain (or vice versa to get full from empty), you need a cover property that captures the fact that either action is possible – that these behaviors can happen and are not mandated to always happen. In the above example, we have used the SV liveness operator ‘##[0:$]’ to express that a behavior captures something that should eventually happen, which is the intent here.
It must be pointed out that formal tools do not require any work for the user on stimulus generation. Formal property checking tools do that ‘for free’. The only thing to keep in mind is how to prevent illegal stimuli being driven into the DUT. This is done by encoding sensible user-driven constraints as assumptions on the DUT. Thus, by using the assume property, one can express the environmental constraints required to verify a DUT with respect to requirements.
Methodology matters
A good methodology is fundamental to successfully using formal property checking in a scalable way that guarantees a higher ROI. Here are some of key factors in developing one:
- Requirements: Having well-specified requirements is one of the most important aspects of any verification methodology and has a great impact on the quality of formal verification. First, describe requirements to capture what the design does. Then focus on how the design does it. A number of things here need to be understood and then specified.
- What needs checking?
- What needs to be assumed of the environment driving the DUT’s inputs?
- Define the ‘must happen’ behaviors and the ‘could happen’ behaviors.
- Define the ‘must NOT happen’ behaviors to rule out any unintended behaviors of the design.
- Abstraction: Using abstraction allows you to mask complexity and focus on what really matters. This is another big topic and the reader in interested in taking a deeper dive should look at this recent overview. It describes an abstraction-based methodology for large-scale verification. It also provides a survey on the history of abstraction.
- Coverage: Knowing when a verification task is adequate and can be signed-off as complete is one of the biggest challenges in modern-day formal verification. Several commercial formal verification tool providers have a solution to this; however, the use model varies from one tool to another, and, depending on which tool the user is deploying, the results vary. This divergence in seeing the same problem in different ways is not healthy for the end user. We will cover more on this in a later article.
In a nutshell, the use of formal property checking to find bugs and achieve comprehensive rigor in building exhaustive proofs relies on multiple factors, such as powerful mathematical solvers, good methodology, and the ability to sign-off your verification.
What’s Next in Formal?
I hope you find this high-level introduction to formal verification edifying. Over the two articles, I have highlighted the main areas of formal and their historical evolution leading up to the state-of-the-art formal methods that are currently used in almost all major semi-conductor companies in the market. I have then summarized how practitioners use properties to do ABV, and what other considerations should be kept in mind, such as the role of methodology, abstractions, and coverage when using formal ABV. I could not cover them in great detail in this post—you’d be reading for weeks—but stay tuned to the Doc Formal blog for closer investigations of these and many other facets of formal.
What do I see on the horizon for formal? To keep pace with design complexity and deliver high-quality verification solutions for safety-critical systems in the automotive, avionics, railways, and marine design segments, dynamic simulation alone is inadequate
A good blend of formal and simulation is becoming essential before designs move to emulation, where finding and debugging design bugs can be very expensive and painful. Too many semiconductor companies do not get this right. Emulation is an excellent way of carrying out system-level testing, but not of finding bugs at the module level.
The advent of the Internet of Things has renewed the focus on security for hardware designs. Here again, the sheer number of combinations of scenario means that simulation alone is not enough. The power of formal ABV-based techniques for security verification is already gaining traction, though not yet at the same level as functional safety verification.
I predict that the next five years in verification will continue to be dominated by formal verification even more than the last 20. Evolution will be driven both by requirements for verification, such as safety and security, and by improvements in scalability of mathematical solvers that leverage groundbreaking machine learning techniques. Research in big data and artificial Intelligence is poised to have a significant impact and provide a new way of debugging designs that is significantly faster and provides higher quality feedback. With newer technologies providing much better sign-off capabilities, formal should be used even more to sign-off verification.
Formal verification is here to stay. One need look no further than the past fifty years since the debut of the ACM A.M. Turing Award for the highest contribution to computer science: eight of these prestigious honors have been awarded to pioneers in formal methods. The field of formal verification has influenced, and will continue to shape, some of the greatest advances in verification.
 Ashish Darbari is CEO of formal verification consultancy and training provider Axiomise.
Ashish Darbari is CEO of formal verification consultancy and training provider Axiomise.