Physical verification of finFET and FD-SOI devices
A look at some of the design and physical verification challenges of working with finFET and FD-SOI devices, including their impact on layout, DRC and LVS.
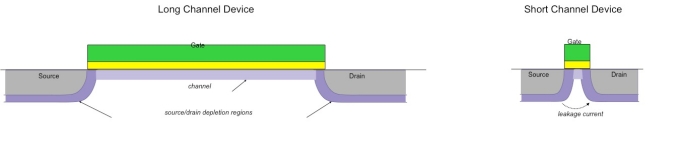
As the minimum dimension of planar transistors has fallen below 90nm, their effectiveness as a true On/Off switch has been undermined by the increasing proximity of the source and drain at either end of the device channel. In such small devices, the length of the transistor’s conduction channel underneath the gate has become comparable to the width of the depletion layer around the source and drain regions, as shown.
Figure 1 A short-channel device's channel length is comparable to the depletion widths associated with the drain and source, so edge effects cannot be neglected
This creates a number of ‘short-channel’ effects, including:
– Threshold voltage roll-off: The threshold voltage of the device is reduced because the depletion regions of the source and drain intrude into the channel, change its effective geometry and therefore make it easier for current to flow from source to drain. The lowered threshold voltage makes it more difficult to turn the transistor fully Off, increasing its leakage current and therefore power consumption.
– Drain-induced barrier lowering (DIBL): As the source and drain get closer together, they become electrostatically coupled, such that the drain bias can affect the potential barrier to current flow at the source junction, increasing the threshold voltage roll-off, and hence the leakage.
– Charge mobility degradation: Atomistic effects such as surface scattering, velocity saturation, impact ionization, and hot-electron effects, reduce the mobility of both electron and hole charge carriers. Device architects have tried various ways to strain the crystal lattice of the channel to make it easier for charge carriers to flow through it, hence restoring its conductivity.
– Threshold voltage variation: This is due to statistical irregularities in dopant concentration, which become significant when the devices are so small.
Short-channel effects have negated many of the benefits of scaling transistors from 28nm to 20nm and have led to concerns about the economic viability of planar semiconductor processes at 20nm and below.
Alternative transistor designs
The industry has responded by suggesting two alternate device architectures, known as finFET and FD-SOI, that mitigate the effects. The finFET moves the channel out of the bulk silicon into a vertical fin and wraps it on three sides with a gate electrode, improving the electrostatic control of the channel. The silicon-on-insulator (SOI) transistor is a planar device whose channel is built in such a thin (shallow) silicon layer that the gate electrode can exercise full electrostatic control of the charge carriers in it.
FinFETs
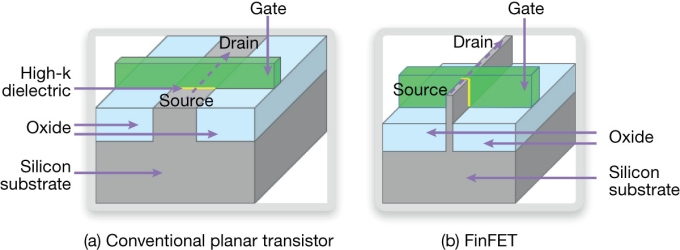
FinFETs (Guide) are built as shown in this diagram.
Figure 2 A finFET’s wrap-around gate is more effective in switching the transistor off, thereby reducing leakage current (Source: Synopsys)
The strong electrostatic control afforded by ensuring that the gate is close to all areas of the channel makes it easier to control the device’s threshold voltage, reducing leakage between source and drain, as well as making it possible to switch it more quickly.
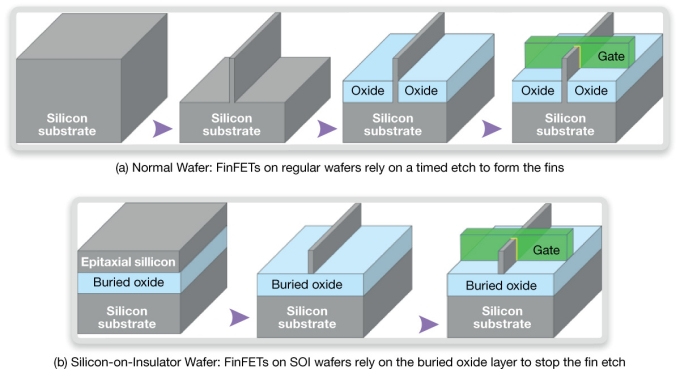
FinFETs can be made on regular silicon wafers, or on SOI wafers, as shown.
Figure 3 FinFETs can be made on bulk silicon or on SOI wafers (Source: Synopsys)
Building finFETs on SOI is simpler than building them in bulk, because the etch process that forms the fin comes to a natural stop when it reaches the buried oxide layer of SOI, rather than having to be controlled by a timed etch process, subject to process variation, in bulk silicon. Building finFETs on SOI may also lead to more rectangular fins with more regular heights, since on bulk silicon the shallow trench isolation oxide that is necessary to insulate one fin from the next can’t be planarized, leading to variability in the height of the fin above the oxide.
The main manufacturing challenges for finFETs are:
– controlling the etch along the edges of these tall structures to generate uniform fin widths and achieve good edge verticality
– uniformly doping the resulting complex 3D surfaces
– depositing all the films used in the gate stack so that they conform to the surface of the fin
Meeting these challenges requires new materials and more processing steps than used in bulk or SOI devices, making them more expensive to produce.
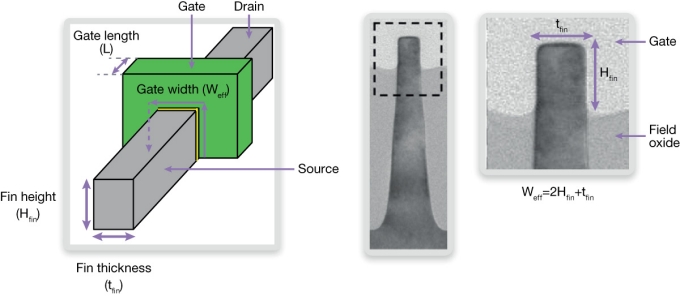
From an electrical perspective, the gate length (L) of a finFET is equal to the thickness of the gate (tfin), while the gate width (Weff) is the periphery of the gate along both sides on the fin plus the thickness of the fin: W = 2 * H + t, as shown.
Figure 4 The electrical dimensions of a finFET, showing the effective gate width W = 2 * H + t (Source: Synopsys)
The fin’s thinness enables strong electrostatic control over the channel’s charge carriers, but limits the number of carriers and hence the channel’s drive strength. To overcome this problem, multiple fins can be connected in parallel, all driven by the same gate. The consequence of the finFET’s topology is that the choice of device width is restricted to multiples of Weff.
Benefits and risks of finFETs
|
Strengths |
Weaknesses |
| Significant reduction in power consumption (~50% over 32nm) | Very restrictive design options, especially for analog – Transistor drive strength is quantized to multiples of a single fin width |
| Faster switching speed | Fin width variability and edge quality leads to variability in threshold voltage VT |
| Effective speed/power trade-off possible with multi-Vt | Extra manufacturing complexity and expense (~+3% according to Intel) |
| Availability of strain engineering | |
|
Opportunities |
Threats |
| Low power makes 20nm technology deployable for mobile applications | The potentially superior electrical performance and simpler manufacturing of fully depleted SOI |
| Increase CPU speeds beyond 4GHz |
Fully depleted silicon-on-insulator
Another way to control short-channel effects in deep submicron transistors is to make planar devices on SOI wafers, forming the channel in a thin silicon layer above the buried oxide. As discussed, the silicon layer is so thin that the gate can influence the whole channel and so completely shut off conduction.
There are two types of SOI devices: partially depleted (PD-SOI) and fully depleted SOI (FD-SOI).
In PD-SOI, the silicon film is 50nm to 90nm thick, so the gate’s influence cannot reach through the channel’s full depth, making the PD-SOI device behave like a slightly better bulk MOSFET.
In FD-SOI (Guide) the silicon film is 5nm to 20nm thick, so that the gate’s influence penetrates the full depth of the channel. The conduction channel doesn’t need to be doped, which eliminates a source of process variability, and the fact that it sits on an insulating layer means there is nowhere for unwanted current paths to form. This in turn relaxes the performance necessary from the gate, and so means that a thicker gate oxide can be used, reducing gate leakage. One advantage of FDSOI over finFETs is that it is possible to back-bias the channels through substrate contacts and so gain even greater control over the threshold voltage.
The primary disadvantage of FD-SOI is the cost of SOI wafers, which is due to the difficulty of accurately controlling the silicon film thickness across the entire wafer. The film thickness is important because the threshold voltage is dependent upon it, so if the film thickness varies across the wafer, so will the device performance. Some manufacturers claim to be able to control the film thickness across a 300mm wafer to within +/-0.5nm.
One drawback of FD-SOI is that it is harder to implement multiple Vt circuitry, which is useful for creating areas of higher-performance or lower-power devices, because it is not possible to alter the channel doping to affect the devices’ threshold voltage. Instead, the threshold voltage is controlled by tuning the gate-stack materials. However, a combination of doping and active biasing can be used to alter the threshold of a target group of transistors that have a common sub-oxide backplane. Another disadvantage of FD-SOI is that it is not possible to selectively strain the channel to improve carrier mobility.
Benefits and risks of FD-SOI
|
Strengths |
Weaknesses |
| Significant reduction in power consumption | High cost of initial wafers (~+10% over regular wafers, according to Intel) |
| Faster switching speed | Limited number of wafer suppliers |
| Easier, standard manufacturing process | Variability in VT due to variations in the thickness of silicon thin-film |
| Availability of back-biasing to control VT | Multi- VT more complex to implement |
| No doping variability | Lack of strain engineering |
| Layout library compatible with existing bulktechnologies | Thin channel limits drive strength |
|
Opportunities |
Threats |
| Simpler and more flexible alternative to finFETs if wafer cost issue can be overcome | High wafer cost threatens economic viability for wider market adoption |
| Better controllability for analog applications |
Designing with finFETs
Layout
Early results suggest that the impact on digital design of using finFETs need not be that great if conservative approaches are taken. It should be possible to migrate circuits created for advanced planar processes to finFETs, using a lot of modeling and simulation to recheck the circuit performance.
One key difference between finFET-based design and that using conventional planar devices is that the freedom to choose the device’s drive strength is reduced as the drive strength can only be increased during layout by adding fins. The effective width of the device becomes quantized, and the quantization effect is worse for smaller transistors for which the next step up from the minimum-size device is one that is twice as wide.
In terms of optimization for power, the finFET provides circuit designers with the opportunity to trade leakage for switching speed and create fast/medium/slow versions of the base transistor.
Design rule checking
DRC for finFETs implies fin-related checks – such as of fin width and fin-to-fin spacing – that are similar to regular planar checks. There are also a number of checks that are specific to finFET processes, such as checking that fins and poly are confined to regular, lithographically-friendly pitches in a fixed orientation.
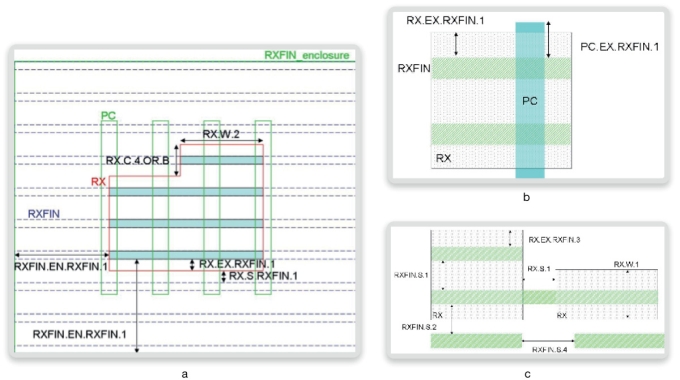
A typical set of finFET physical verification rules contains the elements listed in Table 1 and illustrated in Figure 9:
Table 1 Example of classes of DRC checks for finFET spacing (Source: Synopsys)
RX and RXFIN are drawn layers. RX is drawn as in prior technologies except for some gridding constraints imposed by RXFIN.
RXFIN over RX is ‘active’. RXFIN not over RX is ‘dummy’. An RXFIN will often have portions that are active and portions that are dummy.
Active portions must be surrounded by three dummies. This is enforced through the RXFIN_enclosure rules.
RXFIN_enclosure is a generated shape that encloses a region of fins with a common pitch.
Figure 5 Typical physical parameters used for DRC verification of finFETs (Source: Synopsys)
Layout vs schematic
Device parameter extraction for finFETs is similar to planar devices, including the need to consider layout-dependent effects. Unlike planar devices, the key feature of gate width cannot be measured directly from the two-dimensional layout. The effective gate width depends on the fin height, the distance that the fin protrudes above the oxide surface. However, all the fins are the same height, so Hfin can be entered as a process parameter and used to calculate effective device width, as before.
Another LVS concern for finFETs is the need to accurately extract the source/drain resistance, which forms a significant component of the transistor’s parasitic series resistance.
Designing with FD-SOI
Layout
In principle, it is possible to directly port a cell library from a bulk process on to an FD-SOI process. However, the results will not be as good as dedicated cell libraries designed to take advantage of the different balance of capacitances in FD-SOI devices and the reduced variability of undoped channels.
The SOI Consortium has proposed a ‘safe’ way to adopt FD-SOI, using hybrid FD-SOI/bulk co-integration. In this approach, IP cores that are deemed too risky to redesign are placed on to areas of the wafer that expose the bulk silicon, while synthesized logic optimized to use FD-SOI structures is placed on areas of the wafer that retain the buried oxide layer.
The use of FD-SOI could have a significant impact on design if designers take up the opportunity to dynamically back-bias the channel, which gives better control over VT variability and so improves device switching speed.
DRC/LVS
Since FD-SOI is a planar technology, DRC and LVS checking is the same as for existing bulk technologies.
Conclusion
Short-channel effects severely limit the performance of bulk planar transistors at process nodes below 90nm.Two alternative devices are being proposed for process nodes below 20nm: finFETs and FD-SOI. Both are practical solutions that solve the major short-channel difficulties, both have been proven on real designs, and both are backed by major semiconductor companies. It is not yet clear which technology will predominate or if they will continue to co-exist.
In terms of physical verification, both processes are well supported by Synopsys’ physical verification tools. All new physical checks are well within the capabilities of Synopsys’ DRC solution, and the new device parameters can be extracted with Synopsys’ LVS tools.
(To read what attendees at the December 2012 International Electron Device Meeting felt about the relative merits of finFETs and FD-SOI in practice, click here.)
Authors
Marc Swinnen received a Master’s Degree in Electrical Engineering from the Catholic University of Leuven in Belgium and an MBA from San Jose State University. He has over 20 years of experience in Marketing and Technical Support at various EDA companies. Marc has been at Synopsys for 7 years, where he is Senior Product Marketing Manager working with IC Validator.
Ron Duncan is a Sr. Manager at Synopsys in Mountain View, CA. His team supports IC Validator and PrimeYield. Ron has worked at Hewlett Packard, ISS and Avant!, prior to Synopsys. His semiconductor and EDA experience spans physical design and verification, circuit simulation, device design, mask synthesis, TCAD and semiconductor manufacturing. He holds electrical engineering degrees from MIT and Cornell.