Optimizing the hardware implementation of machine learning algorithms

Machine learning (ML) could fundamentally change the way we interact with our devices and live our lives. For this to be possible, we need to capture petabytes of data and move it between edge devices and data centers, and then create mathematical representations of  the data so it can be processed efficiently. We can achieve efficient processing by offloading key ML algorithms from generalized processors into optimized hardware, and this approach is becoming more common as the core algorithms for today’s ML tasks stabilize.

One of the most important current approaches to machine learning is the neural network, a mesh of processing nodes and interconnections that is loosely modelled on the neurons and synapses of the human brain. A neural network can be used to ‘learn’ an output for a given input, for example by training a network to recognize features within an image through a ‘training’ process. In this process the network is exposed to many images that include the features you want it to recognize and is given feedback about the conclusions it draws from those images. For humans, this would be a classroom exercise, and for hardware it involves doing a lot of complex math.

Once a neural network has been trained, the trained network can be used through a process known as inference to analyze and classify data, calculate missing data, or predict future data. Inference is done by taking the input data, applying it to a network of nodes where it is multiplied by ‘weights’ (which are really mathematical judgements on how important that data is to an overall correct conclusion), and then further modified by applying an ‘activation function’, which determines the relevance of the information that the node is receiving.

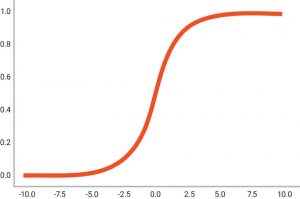
Various activation functions are used, from simple binary step functions to more complex activation functions such as the sigmoid function, S(x) = 1/(1+e^-x). This function produces an S-shaped curve in which S(x) = 0 as x approaches -∞ and S(x) = 1 as x approaches +∞. When x = 0, the output is 0.5, as shown in Figure 1. Values greater than 0.5 can be labelled as a ‘yes’ and values less than 0.5 can be labelled as a ‘no’, or the function can be used to indicate the probability of a yes or no using the value of the curve at a given point. One limitation of the sigmoid function is that when values are greater than +3 or less than -3, the curve gets quite flat and so calculations need to be done at very high precision in order for a neural network to continue learning during the later stages of the training process.

It’s not yet clear whether effective neural networks need to work to floating-point (FP) precision, with all the complexities this brings to hardware design. Today’s neural-network predictions often don’t require the precision of 32bit or even 16bit FP math. In many applications, designers can use 8bit integers to calculate a neural-network prediction that is accurate enough to serve the recognition task effectively.

Controlling neural network precision with IP

The DesignWare Foundation Cores library of mathematical IP offers a flexible set of operations with which to implement ML math. The library enables designers to trade off  the power, performance, and area of a neural-network implementation by controlling the precision with which it does the necessary math .

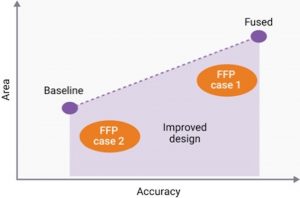
To illustrate this, compare a simple, baseline multiplier with a ‘fused’ or pre-built multiplier that can handle multiple precisions, as shown in Figure 2.

For both integer and FP operations, designers can control internal or inter-stage rounding between operations. For FP operations, designers can also create efficient hardware implementations by sharing common operations using internal rounding control and the flexible floating-point (FFP) format. This format enables designers to build specialized FP components, and then ensure they will meet their design’s requirements by using bit-accurate C++ models to explore the resultant components’ accuracy, area and likely power consumption.

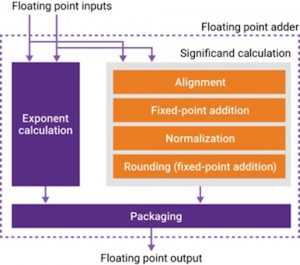
FP algorithms are usually implemented by combining a number of basic, or ‘atomic’ sub-functions. For example, consider the simple block diagram of a FP adder shown in Figure 3.

There are two main paths in an FP adder to calculate exponents and significands. These two paths exchange information to generate the result. When the significand is scaled, the exponent is adjusted accordingly.

The main mathematical sub-functions used in significand calculation are alignment, fixed-point addition, normalization, and rounding. Normalization makes up a large percentage of the logic of an FP adder, so eliminating it would cut die area and power. Doing without normalization, however, could cause the loss of significand bits, with a potential impact on the overall accuracy of the resultant calculations.

Internal values of the significand are represented in a fixed-point format, and are tightly connected with exponent values in the exponent calculation path. To implement sub-functions, there needs to be a way to carry exponent and fixed-point significands together, as is done in standard FP systems, but with fewer constraints and special cases.

If a calculation demands a sequence of FP additions, normalization and rounding steps will make up a lot of the hardware’s critical path. With this kind of compound operation, it is usually best to leave normalization and rounding to the final stage, because having direct access to the internal fixed-point values of an FP operation, without normalization or rounding, reduces the implementation’s complexity, area, and critical path as well as giving designers control over its internal precision.

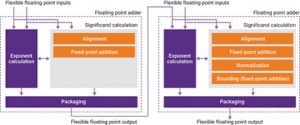
A simple example of a two-stage adder is shown in Figure 4. By eliminating the normalization and rounding stages, the numerical behavior of this adder changes. First, the exponent calculation is simplified in the first FP adder. Second, the representation of the first FP adder’s output does not comply with the IEEE 754 FP standard anymore. This means that third, the second FP adder in the chain needs to understand this new representation and to have information about what happened in the previous calculation in order to make its decisions.

Synopsys’ DesignWare Foundation Cores includes configurable components that can be used to develop larger IP blocks. As each component is configured, its RTL and C models are installed into a project directory that includes all the files associated with the verification and implementation of the components. Once the design is complete, the files integrate into the larger SoC design and designers can continue to refine their RTL for the next generation of the product.

Summary

The current rapid uptake of machine-learning strategies is driving the development of a new class of devices and services that interact with the real world. For many of these devices, and especially for those designed to operate at the edge of the network, the efficiency with which they can carry out the underlying math of machine learning will be a critical differentiator.

Designers who want to explore complex trade-offs between various algorithmic strategies, types of number representations, data accuracies, rounding strategies and more need access to a set of configurable building blocks with they can explore their design space. Synopsys’ DesignWare Foundation Cores give designers these blocks, and support their design exploration with bit-accurate C++ models as well as RTL that can be incorporated in larger IP blocks and the wider SoC.

Further information

Web: DesignWare Foundation Cores

Author

John A Swanson, senior product marketing manager, Synopsys

Company info