Win on the fault campaign trail with formal
How formal verification for the ISO26262 automotive functional safety delivers the full activation, propagation, and observation in the form of proven and exhaustive results.
Making cars safer has been an important design concern since the first automobile-related fatality in the 19th century. Hydraulic brakes, safety glass, seat belts, and air bags are just some the hardware components invented to make cars safer. And it was not long before barrier crash tests and the iconic crash test dummies came to represent rigorously controlled experiments that validate the effectiveness of these features.
Today, in addition to an entirely new set of safety devices, the digitalization of automobiles has introduced procedures and requirements that focus on the safety performance of electronic and electrical systems. These have been codified in the ISO 26262 automotive functional safety standard, the 21st century child of the crash test.
ISO 26262 requires that electronic devices for automotive applications perform random hardware failure analysis to ensure that a bug in a chip will not result in injury or harm. In what is known as a fault campaign, simulators are used to randomly inject faults to test the correct functionality of a component’s safety functions and mechanism.
The problem is that fault injection during simulation can be time consuming and exacting work. Worse, it does not guarantee that faults are propagated for testing. These reflect the two major challenges to a successful fault campaign: reducing the number of faults that need to be activated and propagating the fault through the design.
Formal verification does a better job than simulation of overcoming these issues by using structural analysis to easily categorize faults for diagnostic coverage and by analyzing faults to verify propagation, safety goal violations, and fault detection.
Let’s take a look at why formal is a better way to conduct a four-step functional safety fault campaign and how it mitigates obstacles along the way.
Prepare for the campaign: Know Your Stuff
First, some background. A fundamental difference between the hardware and electronic safety features of the 19th and 20th centuries and those of our digital age is that the former involved discrete components. That made it easy to distinguish between a safety and a non-safety component. A seat belt was for safety. A seat was for comfort (well, maybe not so much at first).
Formerly, electronics in cars were treated as black boxes—when a part fails, the part is swapped out. But modern technology allows us to squeeze so much into an IC that we end up mixing safety and non-safety logic together. So, the entire design becomes a safety component. For example, registers may be shared between different safety and non-safety related parts of the design. The blurring of these lines between further complicates the effort to satisfy ISO 26262 because only safety-related elements should be used in calculating fault metrics.
Instead of identifying safety elements in an IC (since logic probably spans multiple modules), it is easier to identify safety critical paths that when combined together form the safety goal or safety function. Likewise, a fault may be detected by multiple safety mechanisms, any of which may amount to the fault being detected or perceived. Therefore, on an IC, the idea of a safety element has less to do with module boundaries and more to do with related safety logic, perhaps more accurately referred to as a safety domain.
The only way to justify removing non-safety related logic is to show there is independence between the safety and non-safety logic. This can be done using a dependent failure analysis. Proving independence, however, is typically not easy, and including all design logic means injecting more faults than necessary, which will most likely dilute diagnostic coverage, which represents the percentage of the safety element that is covered by the safety mechanism.
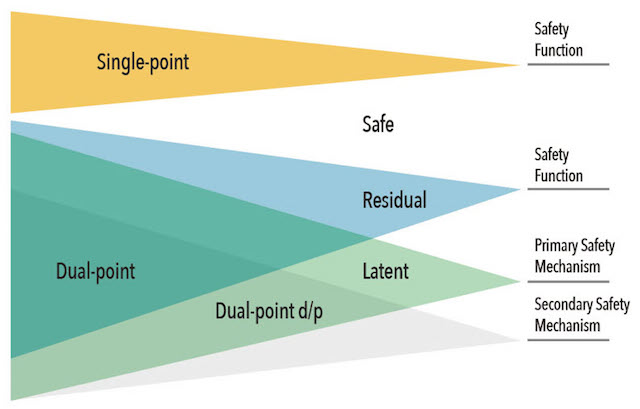
Diagnostic coverage is computed by first determining the number of different types of faults in a design. What we are looking for are faults that are either unprotected by any safety mechanism (known as a single-point fault) or are supposed to be covered but that a safety mechanism fails to detect (referred to as a residual fault). If a fault is injected that has no impact on the safety-critical functions or can be detected by the car driver, it is considered safe.
The ISO standard addresses potential faults in the safety mechanism. Typically, an automotive design will have a secondary safety mechanism to check the behavior of the primary safety mechanism. In order to test the safety mechanism is correct, a fault must be injected into the design to activate the primary safety mechanism, and then a second fault injected into the primary safety mechanism to see if it still works. This is referred to as a dual-point fault. Any dual-point fault not covered by the secondary safety mechanism is considered latent. Once all the faults in a design are classified, then the ISO 26262 metrics are easy to compute.
On to the campaign trail
A fault campaign has four essential steps:
- Activation
- Propagation
- Observation
- Results reporting
Let’s look at each of those.
First, faults need to be activated. In an RTL design, all nets, registers, and ports are possible faults. While this is a lot of faults, there are many times more in a gate-level netlist (in the millions). The number of possible faults becomes astronomical when considering dual-point faults for latent fault analysis. In practical terms, simulation takes too long to possibly test all faults. Instead, a random sampling of potential faults is chosen (usually several thousand) and simulated in order to give a statistically acceptable margin of error in the campaign results.
The second step is to propagate the fault through the design. While regression tests can be used for fault injection, extra effort should be made to ensure that the faults actually propagate. For example, if the design logic is in the wrong state, then propagation of the fault may not be possible. This requires either a bit of manual effort and inspection and use of coverage metrics, or turning a blind eye to the fact that the tests selected may have been totally useless. In other words, simulation results may provide high confidence from a statistical sampling perspective, but they do not provide high confidence that the results are actually meaningful.
The third step is to observe the fault, or indicate that the fault has been controlled or detected. Testbenches are great at checking and indicating failures; however, this can become a hindrance in a fault campaign. Injecting random faults means that the simulation may go off into the weeds and exhaust itself before the fault can even propagate to be detected. Often, tests are compared with a golden simulation waveform (i.e., one without the fault injected), and the test is considered a failure if the safety outputs differ. The problem here is with the assumption that a different output implies a fault. It is also possible that injecting a fault causes the design to go down another path that is nevertheless legal. Likewise, the safety functions and mechanisms may differ in the waveform, but the safety mechanism may actually detect the failure. The test may be marked as failing when in fact it should be considered successful. Conversely, a test may end with a passing result because no checker fired, but the fault went undetected so the test should be counted as a failure. Therefore, results need to be interpreted, as well as the ‘fault detection interval’ (FDI) considered, which specifies a maximum amount of time for a fault to propagate to detection before it is considered unsafe.
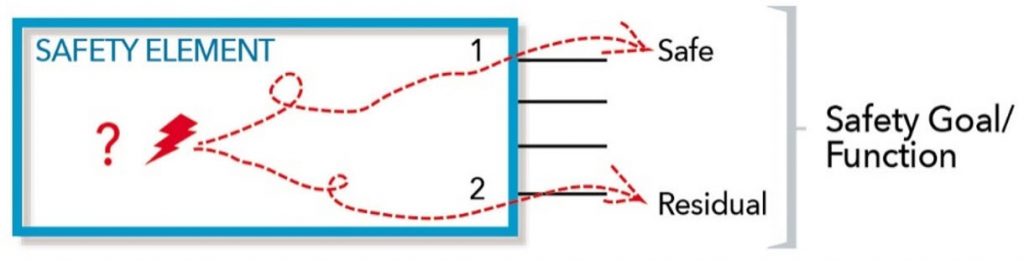
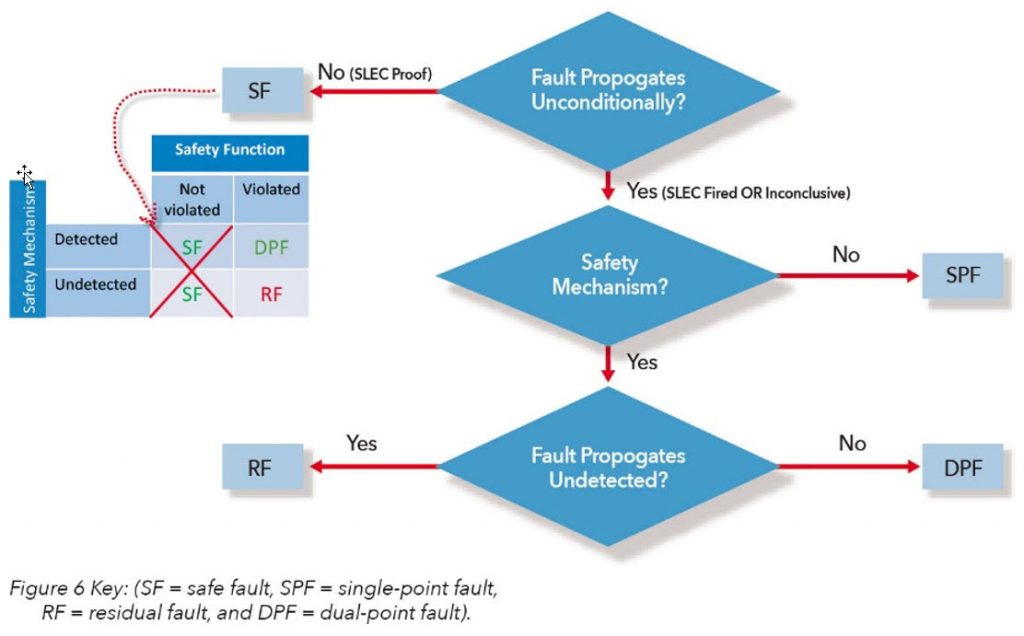
The fourth step is to report the results. In an IC where resources are shared, the results of the fault injection need to be merged. For example, suppose a safety function is composed of multiple safety critical paths through the design, as shown in Figure 1. The fault has no impact on path 1, which would imply the fault is safe. However, down path 2, the fault goes undetected by the safety mechanism, i.e., it is a residual fault. In this example, the residual fault of path 2 would have priority over the safe results of path 1 so the merged result would be considered as a residual fault. The priority of the faults can be inferred from the flow chart B.2 in the part 5 of the ISO standard [2].
Targeted damage control
Reducing the number of faults that need to be activated is the first major challenge in a fault campaign. Formal structural analysis tackles this issue by significantly pruning the number of faults required for analysis.
Formal synthesizes a design into a Boolean representation in order to perform its analysis. The size of the design does not matter, but only that the design is synthesizable. This enables the formal tool to trace back the cone of influence of a signal; i.e., all the logic that can possibly affect it. In the context of a random hardware failure analysis, a cone of influence (COI) can automatically prune out all faults that are structurally safe without requiring further analysis since anything outside of the cone is by definition classified as a safe fault, as shown in Figure 2. Further, the cones of influence can reveal what logic is covered by a safety mechanism or not, indicating single-point, residual, and latent faults. This structural analysis provides a quick classification before any fault injection is performed, which provides a worst-case or best-case scenario for the diagnostic coverage calculation.
Further structural fault pruning can be done by looking at the minimum number of cycles that faults require to propagate through the design. If the propagation time is greater than the fault detection interval or multi-point fault detection interval specified by hardware requirements, then it is by definition undetectable and classifiable without further analysis. Additional faults can be pruned by constraining the design, which will cause the formal synthesis to prune logic just like a synthesis tool. Lastly, given the appropriate formal engine, faults could be collapsed if they can be proven to be structurally equivalent or dominant, much like an ATPG algorithm.
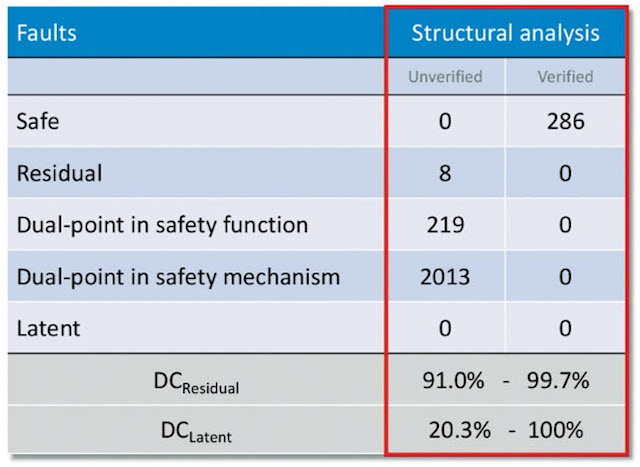
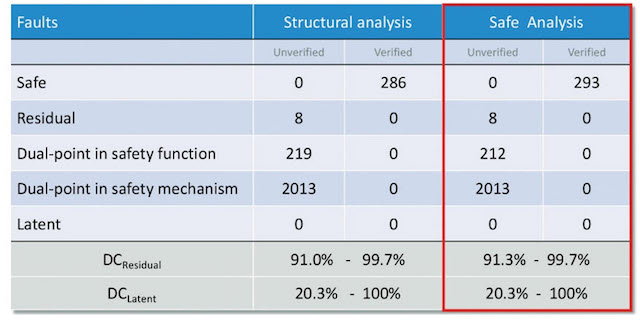
Structural analysis is typically pretty quick. It results in a worst-case/best-case diagnostic coverage calculation, an example of which is shown in Figure 3.
In this example, 286 state bits reside outside of the cone of influence in the RTL module so they are automatically classified as safe. Other state bits are classified as residual or dual-point faults, but without further analysis, it is not verified. They are marked as unverified because structurally they may look like a particular type of fault, but there is no guarantee once the fault is injected that it will affect the safety goal or be detected. To move these faults into the verified category, formal analysis needs to be performed. Assuming the worst case scenario that all the dual-point faults in the safety function are residual, a worst-case residual diagnostic coverage can be calculated. Likewise, assuming all dual-point faults in the safety mechanism are latent, a worst-case latent diagnostic coverage can be computed. That means that if your safety ASIL goal is only ASIL-B (90%), then no further analysis is required for residual faults since structurally the coverage cannot be worse than 91%. On the other hand, a latent diagnostic coverage of 20% is below an ASIL-B level (60%) so latent fault analysis is necessary.
Guaranteeing fault propagation
The second major challenge in a fault campaign is propagating a fault through the design. Proving that a fault really propagates through a design in simulation is not a trivial matter. With formal, however, fault propagation is guaranteed.
Formal exhaustively traverses through the state space, finding whatever path possible to prove or disprove whether a fault can propagate. No manual inspection, hand-crafting of tests, or writing of covergroups is required to guarantee that the fault sensitized the path to the safety function or safety mechanism. Better yet, formal does not require stimulus to be given to it, nor is a testbench required. The formal tool automatically determines the stimulus. In traditional formal verification, formal exhaustively goes down all paths, including illegal or undefined states, which results in false negatives. For fault propagation, however, a specialized formal technique called sequence logic equivalency checking (SLEC) can be used.
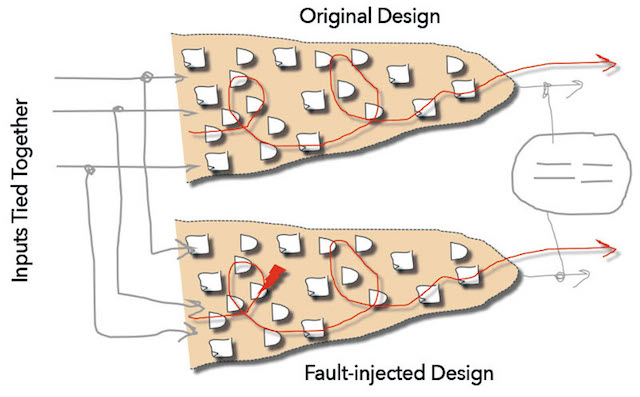
SLEC can be used to prove two designs are equivalent, but unlike LEC (logic equivalency checking), which checks only that the combinational logic between registers is equivalent, SLEC checks that the functional outputs of two designs are equivalent. In other words, the designs can be implemented totally differently with different internal timing as long as their outputs are the equivalent. SLEC automatically ties the inputs together, applies the stimulus, and then checks that the outputs are the same. SLEC has many uses like checking that a design was ported from VHDL to Verilog correctly, or that adding extra logic to a design does not affect the main functionality (like the use of chicken bits).
In a fault campaign, SLEC provides the mechanism to constrain the inputs without any user input. The design under test is compared with itself, and a fault is injected into its other instance. If the fault does not cause the outputs to change (i.e., the two instances are equivalent even when the fault is injected), then the fault cannot violate the safety goal and is proven safe. Since the inputs are tied together, the formal inputs are constrained by the original design; i.e., only legal values through the design can be sent through the error-injected instance. This eliminates any hand-crafted tests or constraints, and the state space can be exhaustively explored. This kind of propagation is shown in Figure 4.
Injecting the fault with formal simply requires creating a conditional cutpoint. A cutpoint is a net or register whose driver has been removed that becomes a formal control point, which can be used to create a stuck-at or transient fault. SLEC also allows the use of cover properties so you can specify that when a specific fault is injected, a safety goal violation occurs and it is detected within a specified time interval.
The analysis
Fault analysis using formal SLEC can be broken into three steps:
- Safe fault analysis
- Residual fault analysis
- Latent fault analysis.
Safe fault analysis is where a fault is injected and checked to see if it propagates through the design unconstrained. If the outputs remain equivalent, then the fault is proven safe. This is an easier proof for formal since residual fault analysis requires checking for a safety goal violation that is not detected within a specific time interval. Unconstrained SLEC is usually pretty fast, but most faults within a cone of influence are likely to have some effect on a safety output. As shown in Figure 5, the safe fault increases since some of the dual-point faults in the safety function have been proven safe.
Next, residual fault analysis is performed using SLEC to see if all the dual-point faults in the safety function can be detected (Figure 6). Anything not detectable means that it is not covered by the safety mechanism and is therefore a residual fault.
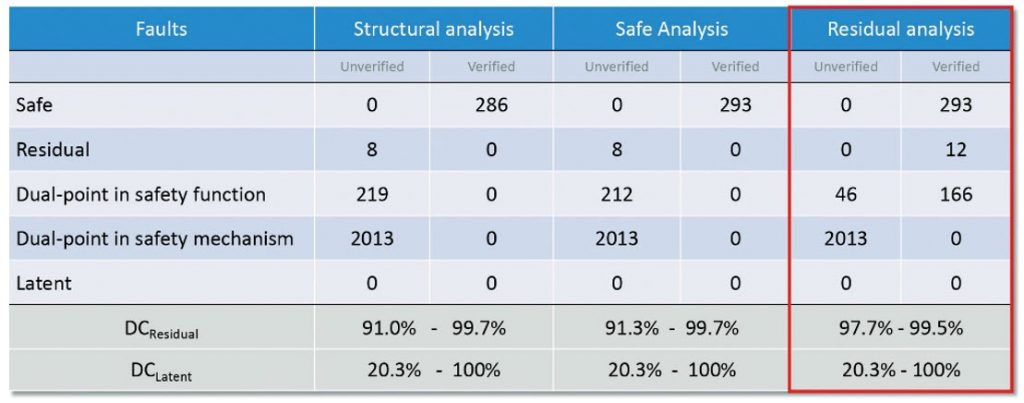
Figure 7 shows how, as the faults are verified, some may be proven to be residual or detectable, which narrows the range for the residual diagnostic coverage.
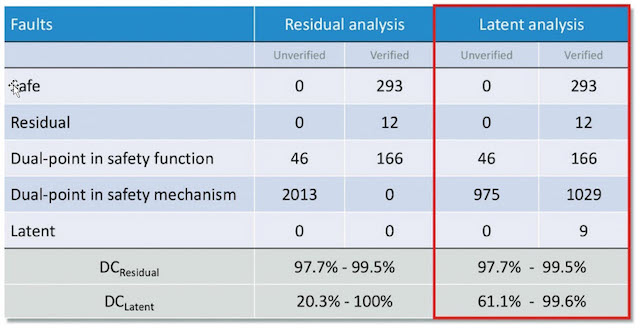
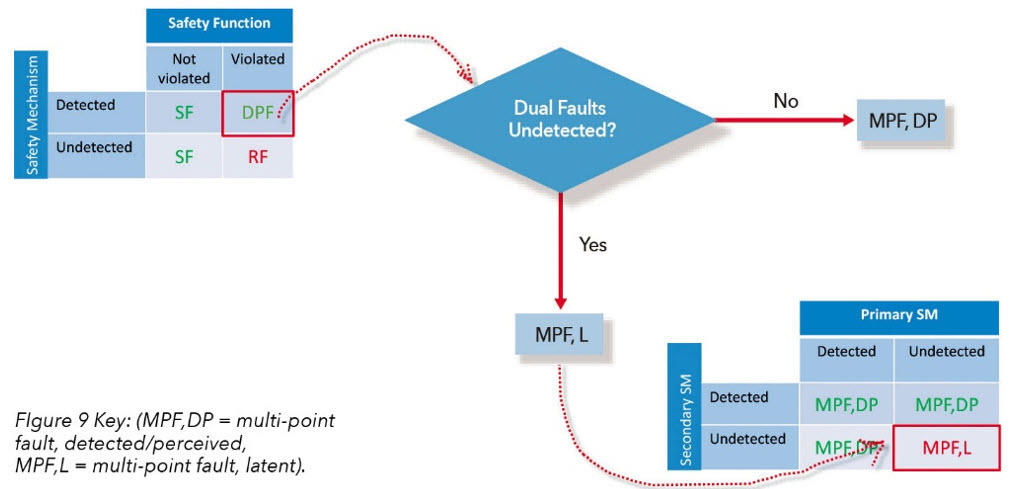
Figure 8 shows how as dual-point faults in the safety mechanism are verified as detectable, the latent diagnostic coverage range narrows to a more acceptable level. The flow is described in Figure 9.
A winning campaign for ISO 26262
A formal-based flow has the advantage of producing a diagnostic coverage range upfront in your fault campaign. Faults are guaranteed to be activated, propagated, and observed, and the results are proven and exhaustive. Unlike simulation or emulation, which can only produce best-case results based on limited time and test inputs, formal technology provides guaranteed worst-case safety metrics because it explores all of the state space. With that in mind, would you rather ride in a car engineered for the worst-case or best-case scenario? Clearly there is no better way to run a fault campaign for ISO 26262 than with an automated formal-based methodology.
About the author
Doug Smith is a functional verification consultant for Mentor-Siemens based in Austin Texas with expertise in UVM and formal technologies. He has provided both formal and application engineering support while at Mentor, offering tool, language, and verification methodology support across the Questa simulation and formal functional verification platforms.
Doug holds a masters degree in Computer Engineering from the University of Cincinnati.