Achieving teraflops performance with 28nm FPGAs

Introduction

Altera’s 28nm Stratix V FPGAs have a new variable-precision DSP architecture that supports both fixed- and floating-point implementations. However, fully exploiting this with existing tools is no easy task. Verilog and VHDL offer meager support for floating-point representations, and there are no synthesis tools to support such work. Meanwhile, traditional approaches to floating-point processor design do not work with FPGAs.

In response, Altera has developed a ‘fused-datapath’ toolflow that accounts for the hardware implementation issues inherent in FPGAs to enable builds of floating-point datapaths. Designers can thus realize high-performance floating-point implementations in large designs that, for Stratix V devices, reach a 1 teraflops processing rate. The toolflow also works well with other Altera FPGA families, such as Stratix II, III and IV as well as Arria and Arria II. Altera has used the toolflow internally to build floating-point intellectual property (IP) and reference designs for several years. In addition, the IP for Stratix IV floating-point performance is already available to designers.

Coupled with the variable-precision DSP architecture, designers now have the option to ‘dial’ a DSP block to a required precision. There is support for existing 18×18- and 18×25-bit fixed-point applications, but there are now also 27×27- and 54×54-bit modes that can support single- and double-precision floating-point applications. The efficiency of the new variable-precision DSP block is critical to achieving 1teraflops performance.

New levels of DSP resources

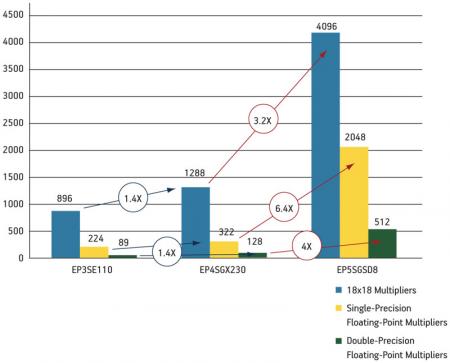
The floating-point processing rates are limited by multiplier resources. Altera multiplier densities have progressively increased with each successive device family. Single-precision multiplier density has increased over six times from Stratix IV FPGAs to Stratix V FPGAs (Figure 1).

The density and architecture of Stratix V FPGAs are optimized for floating-point applications. But a floating-point design flow, such as the fused-datapath toolflow, is also required.

For conventional floating-point implementations in a microprocessor, the input and output data structure for each instruction conforms to the IEEE 754-2008 Standard for Floating-point Arithmetic (2). This representation of numbers is very inefficient to implement within an FPGA because it does not use the ‘two’s complement’ representation usually well suited to digital hardware projects. Instead, the sign bit is separated, and there is an implicit ‘one’ that must be added to each mantissa value.

Specially designed circuitry is necessary to accommodate this representation, and that is why microprocessors or DSP blocks are typically optimized for either fixed- or floating-point operations, not both. Furthermore, in a microprocessor, there is no knowledge of the floating-point operations before or after the current instruction, so no optimization can be performed in this regard. This means the circuit implementation must assume that the logic-intensive normalization or denormalization must be performed on each instruction data input and output.

Because of the inefficiency resulting from these issues, virtually all FPGA-based designs today opt for fixed-point operations, even when the algorithm being implemented would work better with the high dynamic range of floating-point operations.

FPGA-specific optimizations for floating-point operations

FPGAs have characteristics that microprocessors lack, and that can be leveraged to produce a more optimal floating-point flow. Unlike microprocessors, they have thousands of hardened multiplier circuits. These can be used for mantissa multiplication and as shifters.

Shifting of the data is required to perform the normalization to set a mantissa decimal point, and the denormalization of mantissas needed to align exponents. Using a barrel shifter structure requires very high fan-in multiplexers for each bit location as well as routing to connect each of the possible bit inputs. This leads to very poor fitting, slow clock rates and excessive logic usage, discouraging to date the use of floating-point operations in FPGAs.

However, an FPGA has the ability to use larger mantissas than in the IEEE 754 representation. Given the presence of variable-precision DSP blocks that support 27×27 and 36×36 multiplier sizes, these can be used for 23-bit single-precision floating-point datapaths. Using configurable logic, the rest of the circuits can by definition be made to whatever mantissa size is desired. Using a mantissa size of a few extra bits, such as 27 bits instead of 23 bits, allows for extra precision to be carried from one operation to the next, significantly reducing normalization and denormalization steps.

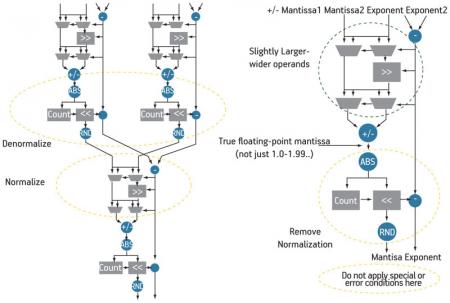
Figure 2 (p. 48) shows how the fused-datapath tool analyzes the need for normalization in the design, and inserts such stages only where necessary. This dramatically reduces any call on logic, routing and multiplier-based shifting resources. It also results in much higher achievable clock rates (f_MAX) even in very large floating-point designs.

Because an IEEE 754 representation is still necessary to comply with the floating-point world, each Altera floating-point function supports the interface at its boundary, whether it is a Fast Fourier Transform (FFT), matrix inversion, sine function, or a custom datapath specified by customers. But whether the fused-datapath toolflow gives the same results as the IEEE 754 approach used by microprocessors and how the verification is performed is open to question.

Even microprocessors can offer differing floating-point results, depending on how they are implemented. The main reason for differences is that floating-point operations are not associative (something that can easily be proved by writing a program in C or MATLAB to sum up a selection of floating-point numbers. Summing the same set of numbers in the opposite order will result in a few different least significant bits (LSBs)). To verify the fused-datapath method, the designer must discard the bit-by-bit matching of results typically used in fixed-point data processing. The tools allow the designer to declare a tolerance and to compare hardware results output from the fused-datapath toolflow against results from a simulation model.

Data comparison

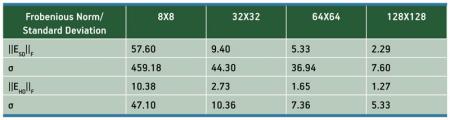
A large single-precision floating-point matrix inversion function is implemented using the fused-datapath toolflow (3), and tested across different-size input matrices. These results are also computed using an IEEE 754-based Pentium processor. Next, the reference result is computed on the processor, using double-precision floating-point operations that provide near-perfect results compared to single-precision architectures. By comparing the IEEE 754 single-precision results and the single-precision fused-datapath results, and computing the Frobenious norm of the differences, it can be shown that the fused-datapath toolflow gives more precise results than the IEEE 754 approach, due to the extra mantissa precision used in the intermediate calculations.

Table 1 lists the mean and the standard deviation/Frobenious norm where the ‘SD’ subscript refers to an IEEE 754-based single-precision architecture in comparison with a reference double-precision architecture, and the ‘HD’ subscript refers to a hardware-based fused-datapath single-precision architecture in comparison with a reference double-precision architecture.

Fused-datapath example

The fused-datapath toolflow has been integrated into Altera’s DSP Builder Advanced Blockset. The design environment for the fused-datapath toolflow, as part of DSP Builder, is Simulink from The Mathworks. This allows for easy fixed- and floating-point simulations.

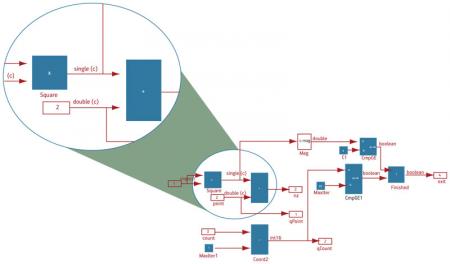
The design shown in Figure 3 was built using floating-point types in DSP Builder. It is a simple iterative calculation for the Mandelbrot set. The Mandelbrot set is defined as the set of complex values of c for which the orbit of 0 under iteration of the complex quadratic polynomial remains bounded (i.e., a complex number, c, is in the Mandelbrot set if, when starting with z(0) = 0 and applying the iteration repeatedly, the absolute value of z(n) never exceeds a certain number (that number depends on c) however large n gets). Since this is an iterative recursive algorithm, it requires high dynamic-range numerical processing, and is a good candidate for floating-point operations.

The subsystem doing the basic math functions illustrates how floating-point complex types—for both single- and double-precision architectures—are used in conjunction with fixed-point types. The tool then offers a single environment for building mixed floating- and fixed-point designs, and offers abstraction of complex numbers and vectors, making design description clean and easy to change. All issues related to dealing with mantissas, exponents, normalizations and special conditions are abstracted away, similar to a floating-point software flow.

Math.h functions include the simple operations expected in a simple C library— trigonometric, log, exponent and inverse square root, as well as basic operators such as divide. These are:

• SIN
• POW(x,y)
• COS
• LDEXP
• TAN
• FLOOR
• ASIN
• CEIL
• ACOS
• FABS
• ATAN
• SQRT
• EXP
• DIVIDE
• LOG
• 1/SQRT
• LOG10

The implementation is multiplier-based because Altera FPGAs have an abundance of high-precision multipliers. Traditionally, CORDIC implementations have been used for such operations, but the rationale for this choice is based on the outdated ASIC idea that logic is very cheap and multipliers relatively expensive. For floating-point operations on an FPGA, multiplications are now cheap and have the advantages of predicable performance, low power and low latency. Contrary to accepted wisdom, the multistage CORDIC approach is a highly inefficient method to build these functions.

One of the most common functions requiring high dynamic range is matrix inversion. To support this, the fused-datapath library has a linear algebra library, which includes the following functions:

• Matrix multiply
• Cholesky decomposition
• LU decomposition
• QR decomposition

More linear algebra and vector functions will be added over time. The comprehensive library support of the fused-datapath toolflow within the DSP Builder Advanced Blockset allows customers to build large, complex and highly optimized floating-point datapaths. In addition, fixed- and floating-point operations can be easily mixed within the same design.

Achieving 1teraflops performance

Building high-performance floating-point systems requires the appropriate FPGA hardware resources and the fused-datapath design flow. This requires DSP blocks suited to floating-point operations—and lots of them. Stratix V FPGAs offer a plethora of single-precision floating-point multipliers per die. They also require careful mapping of floating-point datapaths to the FPGA architecture, which is performed by Altera’s exclusive software and IP. In addition, major changes in both hardware and software were required to achieve 1-teraflops processing rates on Stratix V FPGAs.

On the hardware side, there is greatly increased multiplier, or DSP block, density. The DSP blocks have the new variable-precision DSP architecture, which allows 18×18-bit, 27×27-bit and 36×36-bit modes, as well as simple construction of a 54×54-bit mode with a seamless trade-off between the configurations. There are also new fused-datapath algorithms that better combine multipliers and logic, and use vector datapaths.

FPGAs are nominally fixed-point devices with the right mix of logic and DSP balanced for fixed-point operations. This usually results in a deficiency of logic to efficiently implement floating-point operations. But logic, latency and routing can all be reduced by more than 50% with fused-datapath technology to bring the balance needed for floating-point operations in line with that for fixed-point operations.

On the software side, Altera offers a comprehensive set of floating-point megafunctions, including FFT, matrix and trigonometric options. Integration of the fused-datapath technology into the DSP Builder Advanced Blockset then provides the capability for large, customized and mixed fixed- and floating-point designs in a toolflow that analyzes, optimizes and compiles datapaths that may fill an entire FPGA.

The Stratix V EP5SGSD8 FPGA contains the following resources:

FPGA logic resources

• 703K logic elements (LEs) or
• 282K adaptive logic modules (ALMs)

Organized as

• 574K adaptive lookup tables (ALUTs)
• 1128K registers

Hardened blocks

• 4096 multipliers (using 18×18 precision) or
• 2048 multipliers (using 27×27 precision)
• 55Mb internal RAM (in 20k blocks)

The Stratix V floating-point benchmark design is not yet available, but the floating-point performance can be conservatively estimated using Stratix IV benchmark designs. Normally, peak floating-point performance benchmarks are set using matrix multiplication. This is because matrix multiplication is formed from vector dot products, achieved by simply cross-multiplying two vectors, and summing the products using an adder tree.

The Altera matrix multiply megafunction, available today in Quartus II design software, has been benchmarked as shown in Table 2. For example, the 64×64-bit matrix multiply operates at 388MHz in a Stratix IV FPGA. This megafunction benchmark uses a fairly large 12K ALM, or 30K-LE floating-point core, yet it is able to close timing at almost 400 MHz. Without incorporating the fused-datapath technology in the core, it would be impossible to achieve this level of performance on a large floating-point design.

This core uses a vector size of 32, meaning that it operates by cross-multiplying vectors of length 32 each clock cycle. There are 32 floating-point multipliers, and an adder tree of 16 in the first level, eight in the second, four in the third, two in the fourth, and finally one adder in the fifth—a total of 31 adders. Along with the 32 multipliers, there are a total of 63 floating-point operations per clock cycle at 388MHz, giving 24.4GFLOPS. Using the first-generation fused-datapath technology in Stratix IV FPGAs, the 12K ALMs and 128 multipliers of 18×18 size are used to achieve 24GFLOPS.

Benchmarking the Stratix V FPGA with its second-generation fused-datapath tools, the improved architecture shows a marked improvement over the Stratix IV. The Stratix V logic has been enhanced with twice as many registers, four per ALM. This is important because floating-point operations tend to be very register-intensive. Doubling the register-to-lookup-table ratio enhances the capability of the FPGA in these applications. Another major innovation is the variable-precision DSP block and the new 27×27-bit mode with 64-bit accumulators. Previous Stratix generations used a 36×26-bit mode instead. The variable-precision DSP block results in a doubling of DSP resource efficiency, relative to Stratix IV FPGAs.

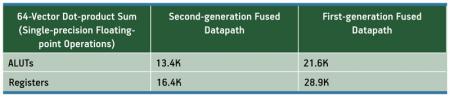
Table 3 shows how the second-generation fused-datapath toolflow achieved significant reduction in logic usage relative to the first generation. A 64-vector dot product uses just a bit more logic than the 32-vector product in the first-generation fused-datapath technology.

The 64-bit vector product sum calculation is 127 floating-point operations, resulting in 49GFLOPS. The benchmarking conservatively assumes that Stratix V FPGAs operate at the same rate as Stratix IV FPGAs.

GFLOPS limitations

Limitations for the Stratix V EP5SGSD8 FPGA are imposed by three resources: logic, registers and multipliers:

Logic limited

• 13.4K ALUTs = 127 floating-point operations = 49GFLOPS
• 574 / 13.4 = 43 vectors
• 43 × 49GFLOPS = 2107GFLOPS

Register limited

• 16.4K registers = 127 floating-point operations = 49GFLOPS
• 1128 / 16.4 = 69 vectors
• 69 × 49 GFLOPS = 3381 GFLOPS

Multiplier limited

• Need 64 multipliers (27×27) per vector
• 2048 / 64 = 32 vectors
• 32 × 49GFLOPS = 1568GFLOPS

The main limiting factor is multiplier resources. This is excellent news for the designer, because it is much more feasible to use 100% of DSP block resources than 100% of logic resources. As the logic usage approaches 100%, timing closure can get more difficult. Also, additional logic is needed to get data in and out of the FPGA to build memory buffer interfaces and other functions.

The basis for the f_MAX is the Stratix IV large matrix-multiply benchmark, which runs at 388MHz. But to be on the safe side, the benchmarking has derated the f_MAX by 20% to about 310MHz. This reduces the GFLOPS per vector product sum by 20%, to about 39GFLOPS. For 32-vector products, this results in 1.25 teraflops, and the following resource usage:

• Multiplier resource usage = 100%
• Logic resource usage = 75%
• Register resource usage = 46%

This analysis, based upon existing Stratix IV benchmarks and fused-datapath technology, shows that an over 1-teraflops floating-point benchmark is achievable. The actual benchmark will be measured against power consumption when Stratix V FPGAs are available, and power efficiency is expected to be in the range of 10 to 12 GFLOPS/W.

Floating-point IP cores

While floating-point IP was first released by Altera in 2009, the associated benchmarks demonstrate that this robust fused-datapath technology has been working and used internally by Altera IP development teams for several years. Altera has an extensive floating-point library of megafunctions. All of these support single-precision floating-point architectures; most support double- and single-extended-precision architectures; and all have IEEE 754 interfaces. The library also includes advanced functions, such as matrix inversion and FFTs. Many of the floating-point megafunctions incorporate the fused-datapath technology. In fact, most of these functions are not practical without the fused-datapath approach.

The Altera floating-point megafunctions are easily accessible within Quartus II software, and incur no additional license fees. They can be found in the arithmetic function library, with the exception of the FFT, which is part of the standard Altera FFT MegaCore function. This FFT MegaCore function incorporates an option for floating-point implementation.

The higher precision of Altera DSP blocks also allows the implementation of floating-point FFTs. These FFTs use the 36×36-bit complex multiply in Stratix IV FPGAs, or the new, more efficient 27×27-bit complex multiply available in the Stratix V family’s variable-precision DSP block. The new FFT compiler enables the designer to choose the floating-point option from an easy-to-use GUI, thus making the code generation of such a complex structure as easy as pushing a button. This FFT core is useful in next-generation radar designs, which are increasingly migrating from fixed- to floating-point implementations, in order to provide greater detection ranges or detection of ever-smaller targets. Achieving the required level of system performance needs the dynamic range of floating-point operations.

Conclusion

The fused-datapath toolflow is a major innovation in FPGA-based DSP technology. It is a synthesis tool capable of generating floating-point datapaths in FPGAs. Coupled with 28nm Stratix V FPGAs, floating-point processing rates in excess of 1 teraflops are now feasible. In addition, a full complement of math.h and linear algebra functions provide full support for complex designs, allowing designers to meet the dynamic range, precision and processing loads required in next-generation DSP applications and products.

References

[1] Altera Floating-point Megafunctions: http://tinyurl.com/ETFdec10Altera1

[2] 754-2008 IEEE Standard for Floating-point Arithmetic:

http://tinyurl.com/ETFDec10Altera2 

[3] Suleyman S. Demirsoy and Martin Langhammer, “Fused-datapath Floating-point Implementation of Cholesky Decomposition,” Proceedings of the ACM/SIGDA International Symposium on Field Programmable Gate Arrays, February 22 – 24, 2009. http://tinyurl.com/ETFDec10Altera3

Altera
101 Innovation Drive
San Jose
CA 95134
USA

T: +1 408 544 7000
W: www.altera.com