Combining algebraic constraints with graph-based intelligent testbench automation

When a constrained random solver generates a stimulus item, its goal is to find one random valid solution to the user’s stimulus description, and this process is iterated until the testbench halts and exits. The more complex the constraints on what can be valid solutions, the harder it is for a purely random engine to produce all the required combinations to thoroughly exercise the device-under-test (DUT).

The main issue here is that, as complexity increases, so does the production of duplicate vectors. Many verification teams consequently spend a lot of time analyzing the missed coverage and manually steering subsequent simulations to try to target the missing cover points. This process can take weeks in some cases.

A more intelligent solution identifies all valid solutions to a set of constraints, given a graph-based description of the stimulus space, and delivers, in a pseudo-random way, those valid stimulus items to the testbench to systematically produce all the combinations needed to meet the coverage goals.

Such a solution can also attempt to meet more than one desired combination at a time from different cross coverage or individual stimulus field targets. As each defined coverage goal is achieved, the generation will automatically revert to purely random values for fields that are no longer involved in the remaining targets.

So, meeting a large total number of cover points, as defined by a number of different cover groups targeting different fields and field combinations, typically requires a number of vectors to be generated that is less than this total. This is in contrast to a purely random methodology, where the number of vectors needed to reach the desired coverage can be anything from 10X the total to, in effect, infinity. This article describes how combining constrained random and graph-based methodologies helps you reach comprehensive verification goals in a more predictable way.

The need for context dependent constraints

A graph-based approach allows for the support of different types of constraints, including a global (or static) constraint that must always be satisfied and a context-dependent (or dynamic) constraint that needs to be satisfied for only specific cases. When a dynamic constraint is declared, the graph structure is used to define the applicable context.

Consider a stimulus generation application for controlling a robot. One field of the sequence item selects a general direction for the motion from between choices such as LEFT, RIGHT, FRONT or BACK. If the chosen direction is FRONT, then the resulting motion must be more in that direction than any other, but there is allowance for some level of sideways component to the vector. Similarly, if the choice is either LEFT or RIGHT then the robot should move more sideways than forward. There are another two fields to determine the new relative position, called xPos and yPos. To ensure that the general direction choice is obeyed in the FRONT and BACK case, a constraint of ‘yPos > xPos’ is placed on these fields in that case. Where the direction is either LEFT or RIGHT there should therefore be the opposite constraint of ‘xPos > yPos’. Therefore, there is a need for context dependent constraints to be specified in the stimulus description.

While the range of xPos and yPos are specified by 12-bit values, only discrete multiples of 64 and 128 can be used for these values respectively. Also, in the special case of direction ‘FRONT’ xPos must also be a multiple of 128. These constraints on xPos and yPos can be implemented in SystemVerilog as follows:

	
constraint xPos_c {
	
    if (dir == BACK) {
	
       xPos % 64 == 0;
	
       xPos < yPos;
	
    } else if (dir ==FRONT) {
	
       xPos % 128 == 0;
	
       xPos < yPos;
	
    } else if 
 (dir == LEFT || dir == RIGHT) {
	
       xPos % 64 == 0;
	
    }
	
}
	
constraint yPos_c {
	
    yPos % 128 == 0;
	
    if (dir == LEFT || dir == RIGHT) {
	
  yPos < xPos;
	
    }
	
}

Yet another field determines the speed, which is either SLOW or FAST. All directions except for BACK can have motion at both these speeds, while the BACK direction is limited to just SLOW.

Defining the stimulus with rules and constraints

One option for a graph- or rule-based description is to simply write a rule, called ‘sel_vals’, that lists the order of selection of the fields of the item. Then the SystemVerilog constraints shown above could be added to the rule description, with one minor syntactic difference of a ‘;’ terminator for the constraint block. The following code shows an example segment of the rules for the Questa inFact tool, with the sel_val rule and the constraint on xPos:

	
symbol sel_vals;
	
sel_vals = dir speed xPos yPos;

	
constraint xPos_c {
	
  if (dir == BACK_ {
	
      xPos % 64 == 0;
	
      xPos < yPos;
	
  } else if (dir == FRONT) {
	
      xPos % 128 == 0;
	
      xPos < yPos;
	
  } else if 
 (dir == LEFT || dir == RIGHT) {
	
      xPos % 64 == 0;
	
In the rule description, we can also define relationships using the graph structure, where a branch in the graph defines the limitations for the BACK, FRONT and LEFT & RIGHT directions. We can also apply dynamic or context-dependent constraints on those branches such that those constraints are obeyed only in the intended context. The lines of code below show the amended rule for sel_vals and the combination of dynamic and static constraints that are needed:
	
constraint xPos_back dynamic {xPos % 64 == 0; xPos < yPos;};
	
constraint xPos_front dynamic{xPos % 128 == 0; xPos < yPos;};
	
constraint xPos_side dynamic{xPos % 64 == 0; yPos <= xPos;};
	
constraint xPos_c {yPos % 128 == 0;};

	
symbol sel_vals;
	
sel_vals =  (dir[BACK] speed[SLOW] xPos_back) |
	
            (dir[FRONT] speed xPos_front) |
	
            (dir[LEFT,RIGHT] speed xPos_side)
	
            xPos yPos;

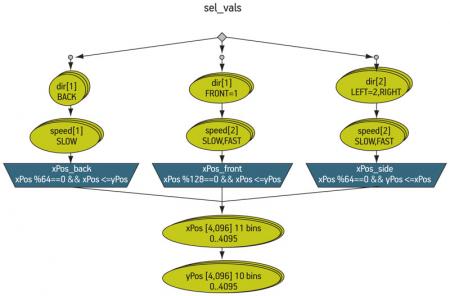
In this example, the ‘|’ choice operator is used to define the optional branches. The first branch limits the direction choice to BACK, limits the speed choice to SLOW, and then applies the dynamic constraint ‘xPos_back’. The next two branches similarly group the related field values and the algebraic constraints that must be applied to fields further down the graph path. The graph branches recombine before the selection of xPos and yPos. Figure 1 (p. 25)shows the graphical view of this rule graph: the dynamic constraints appear in the graph as upside down trapeziums.

Note that in the graph view, there is an annotation on the xPos and yPos nodes stating how many bins are defined for these two fields. Given the large range of possible values, and the limits on which values are legal as defined by the constraints, it is impractical to exercise all 4,096 values. A number of interesting bins are therefore defined for these two fields and the information is used by the intelligent testbench automation (ITBA) tool’s algorithms as they target the user’s coverage goals. Figure 2 shows the definition of the bins for these fields.

The bins declaration follows the declaration of the domain of the field. The last bin uses a ‘*’ to create an additional single bin, which contains all remaining non-explicitly binned values. Bins can also be defined on a per-coverage-goal basis, so that different cross coverage goals with the same variable can be binned differently.

Coverage goals and the stimulus space

The sel_vals rule is one rule within a hierarchy of rules that define the full graph. A higher level rule called ‘RobotCtrl’ includes an initialization step; a construct called a ‘repeat’; some nodes that synchronize the graph execution with the testbench; and another field of the stimulus item called ‘mode’. This code represents the top-level rule:

	
RobotCtrl = init repeat {
	
                pre_fill
	
                mode sel_vals
	
                post_fill
	
                };

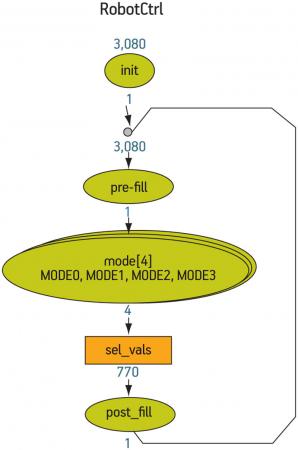
Figure 3 (p. 28) shows the top-level graph. The numbers annotated onto the graph show the size of the stimulus space defined by the elements of the graph, without considering the effect of the constraints.

The total number of 3,080 combinations considers any defined global bins (i.e., those that are not exclusively associated with a particular coverage target). It therefore typically reflects the number of cover points that will be reported for a cross cover group that included all the fields in the graph, prior to the definition of the exclusions due to constraints.

It is of course unusual to attempt to cross every field in the stimulus item, since in most cases that would involve an impractical number of simulation vectors even where sensible bins were defined.

The coverage metrics tend to combine cross coverage targets with individual field targets.

In an ITBA solution, this is achieved by overlaying a user-defined coverage strategy onto the graph. The coverage strategy mirrors the coverage goals by specifying which fields require cross coverage and which are targeted for single-value coverage.

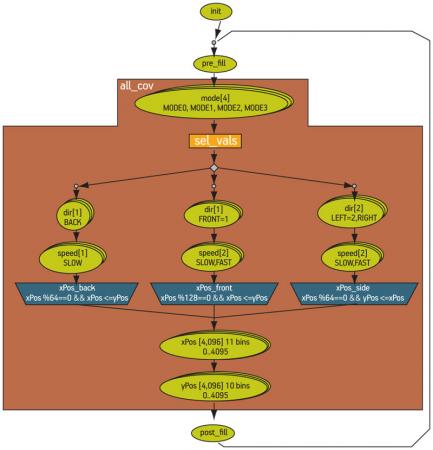
For our robot control verification project, we will assume that the cross of all fields is the goal, so our coverage strategy contains that one goal. A graphical editor can be used to define the region of interest, which goes in the fully expanded graph from the mode node down to the yPos node at the bottom. Figure 4 (p. 28) shows this goal reflected in the graphical editor.

Any of the fields can be excluded by declaring it a ‘don’t care’ for this particular goal. An important benefit of an ITBA tool’s ability to comprehend the graph structure and the constraints simultaneously is that it can report the total number of valid combinations statically, before simulation.

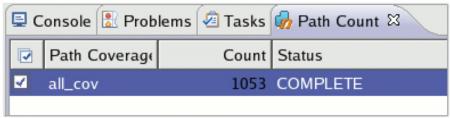
Our example has an additional constraint on the mode field that limits it to just the last three options, so this will also be considered in producing the total valid combinations. Figure 5 (p. 30) shows the result of this calculation that can be performed independently of simulation at the same time as the coverage goals are defined.

While we have 3,520 possible combinations of these field values as binned, the graph structure reduces this number to 3,080, since it reflects the relationship between ‘dir’ and ‘speed’. Then, the constraints reduce the legal set further to just 1,053.

It can be difficult to get to this final number in the presence of many complex relational constraints, and to have the cover group accurately reflect this, but the ITBA tool can calculate this statically very efficiently. By adding just three bins per mode to reflect the constraint on that field, the cover group would contain 2,640 cover points in the cross. Without specifying all the remaining illegal combinations in the cover group definition, the total possible coverage that we can get is 1053/2640 = 39.89%.

Comparing the results

As expected, when the testbench is run with the graph-based approach, all 1,053 legal combinations are created in exactly that number of generated items. The coverage that is reported for the cross is 39.9%. If we define this as the coverage target for a constrained random run a comparison can be made.

As we would expect from a constrained random generation, the progress toward the coverage goals tails off as we get closer to the goal, with significant redundancy in the vectors produced. After 120,000 items, the constrained random generation has hit 1,050 of the 1,053 legal combinations. It takes another 20,000 generated items to raise this to 1,051. A little over another 60,000 items puts us at 1,052, and the final missing combination is achieved after a total of 271,700 items. The effective improvement in the number of vectors it takes to achieve the coverage goal using an ITBA solution is therefore 258X versus the constrained random equivalent. If each vector took a minute to simulate (not an unreasonable estimate) that would mean 17.5 hours of simulation with the ITBA tool driving generation, and 4,528 hours (or almost 27 weeks) with constrained random.

Of course, in a real verification project, other techniques would be used to reach coverage faster, probably in combination. They would likely include multiple parallel simulations, adding directed tests, and writing further constraints to steer the random generation closer to the missing coverage.

What if I cannot control all fields from a graph?

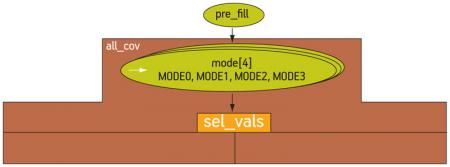
A more complex case is when one or more fields cannot be selected by the graph, but is/are a product of some testbench state. Here, we need to import the externally generated field into the graph to bring awareness of this field value to the tool’s algorithms. With a slight modification to the example Robot control testbench—in fact, two lines of code are affected—we can move the mode field out of the graph’s control and instead randomize it before we call the graph to select the rest of the fields. When a variable is declared as an import in the graph, then its value is read from the testbench when the algorithms traverse through that node in the graph. Figure 6 shows the mode field expressed as an import (denoted by the arrow on the left side of the ellipse).

Note that the domain of the variable is still expressed in the rules, allowing the algorithms to target all the desired values and cross combinations.

In this case a different aspect of the intelligence in the ITBA algorithms is exercised during stimulation, the ability to react to the testbench state when producing a new stimulus item. If the value of mode is imported into the graph, and the coverage strategy is still to produce the cross of all fields, including mode, then an ITBA tool can still far outperform constrained random, taking only 1,340 items to produce all the 1,053 valid items. This is a fairly small overhead.

Do I lose anything?

This is one of the favorite questions posed by verification engineers. After all, random generation produces more vectors than just the ones needed to meet the coverage metrics defined by the user. The generally accepted opinion is that stimulating more vectors is equivalent to more verification. The promise of achieving the targeted coverage in anything from a 10th to a 1000th of the previously required vectors can therefore be a concern. The problem is there is no way to discern if those extra, mostly redundant vectors that were generated before, were actually exercising the DUT in a different or useful way.

There are two ways to respond to this concern. The first requires virtually no extra effort on the part of the verification team. It is to use the ITBA tool to prioritize the needed vectors for coverage and then continue to run the tool in a purely random mode for as long as time and resources allow. A variant of this approach is to target the desired coverage more than once, taking advantage of the fact that the tool will produce different vectors each time in a totally different order. This means that the combinations that the verification engineers thought were of interest get exercised in different contexts.

The second approach assumes that the original verification metrics were not as comprehensive as they could be. Expanding the scope of these metrics does require some effort but it clearly pays off in the confidence level that can be achieved, and as proven in some cases, in the increased number of bugs that are found earlier during verification.

Mike Andrews is a verification technologist specializing in intelligent testbench automation for the Design and Verification Technology Division at Mentor Graphics. His experience includes roles as an ASIC designer, a CAD/design flow specialist and more recently a specialist in hardware/software co-verification and ESL design and verification. He received a Bachelor of Science Degree in Electronics and Applied Physics from the University of Durham in the UK in 1989.

Mentor Graphics
Corporate Office
8005 SW Boeckman Rd
Wilsonville
OR 97070
USA

T: +1 800 547 3000
W: www.mentor.com