Real-number or wreal modeling
Wreal modeling is the colloquial name sometimes given to a behavioral modeling technique – also known as real-number modeling or real-value modeling – that can be used to simulate the functions of analog blocks within a larger predominantly digital simulation. Rather than limiting the data that can be carried by wires within a simulation to a small set of states – typically high, low and indeterminate (X) – the simulation allows the wire to carry a real-number value and so provide analog-like characteristics for modules designed to interpret those values. Wreal is simply short for wire-real – the name used in Verilog-AMS, although both VHDL and SystemVerilog use the variable typename real.
Introduced in dedicated mixed-signal languages and their simulators such as Verilog-AMS and VHDL-AMS, the technique is becoming more widespread among verification teams thanks to its incorporation in standard SystemVerilog. Strictly speaking, nets themselves cannot be real-valued but SystemVerilog supports the concept of real-number variables that can be driven in the same manner as nets – although there can only be one driver. To support the idea of multiple drivers on a net, the simulated block needs to incorporate the necessary functions to derive a functionally correct output value, which have been added to the latest version of SystemVerilog. Vendors such as Cadence Design Systems and Synopsys have added support for multiple drivers to their simulators, and provided the ability in languages such as Verilog-AMS as well as SystemVerilog.
The key advantage of wreal modeling is speed. Models written to generate and use the wreal signals do not have to incorporate solvers but use comparatively straightforward functions to emulate the behavior of analog circuits.
In contrast to work with Spice and the low-level models supported by Verilog-A and other behavioral mixed-signal verification languages in which the solver operates in the analog domain, wreal modeling involves a discrete event solver just that like used for the digital logic. As a resuilt, it does not perform accurately for models that involve significant feedback. However, many blocks can be modeled at a higher level than the feedback circuits often encountered in analog design where this feedback can be abstracted away with reasonable accuracy. As a result, the models are not useful for debugging analog designs themselves but provide a way to ensure that digital logic interoperates with mixed-signal blocks in the full-chip environment.
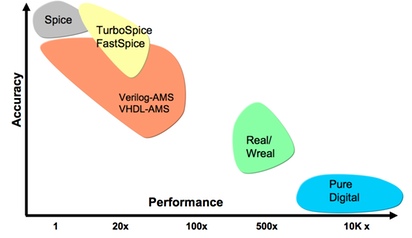
Figure 1 Accuracy versus performance for different mixed-signal modeling strategies (Source: Cadence Design Systems)
The speed-ups can be dramatic according to users and tool providers. Tom Beckley, senior vice president of R&D for custom ICs at Cadence Design Systems, claimed in his keynote at CDNLive EMEA 2012: “The results are stunning: a 300 times improvement in performance if you can move out of Spice and into real-number modeling and event-driven analysis.”
A further advantage of wreal modeling, especially within SystemVerilog, is the ability to use assertions to check that modules are interoperating correctly and also fit well into the verification flows for CPF and UPF.
One stumbling block to the use of wreal modeling is the need for analog designers to generate high-speed but accurate models. Clearly there is a significant risk if models do not accurately capture conditions that can arise in the actual circuit and which would be caught by simulation at the Spice or FastSpice level.
There has been work to develop conceptual frameworks that build on the use of wreal signals to provide not just a methodology for developing robust models but libraries of them that can be tuned for a target design. An example is the program at Stanford University led by Professor Mark Horowitz. He explained the work during his IEEE CEDA talk at 2012’s Design Automation Conference.
R&D is also underway to develop model-generation tools that can take existing analog circuit designs and build behavioral representations. A further avenue of research is into models that better capture the dynamic behavior of analog circuits by not just using functions to generate instantaneous values but also their rate of change and even second derivatives. This could provide better accuracy for circuits with significantly non-linear behavior.
Further reading
Bill Ellersick of Analog Circuit Works has written an overview of techniques used in model development (PDF).