The art of abstraction
Anders Nordstrom is a senior corporate applications engineer in Synopsys’ Verification Group working on formal methodology and features on the VC Formal tool. He has 20 years’ experience in assertion-based verification and formal property verification, in EDA and as a verification engineer. Abstract art uses shapes, color and lines to represent reality without trying to depict it fully. Abstraction had a huge impact on art in the 20th century. It is having a similarly important effect on the formal property verification (FPV) of integrated circuits and systems on chip (SoCs), which have become too complex to address as fully detailed designs. Instead, we can use abstraction, in formal verification as in art, to create a model which resembles reality but with much less detail.
Successful FPV of large designs requires that parts of the design are abstracted. Learning how and where to apply abstractions will result in more proven properties and more bugs found.
The key to successful abstraction in formal verification is to consider what functionality needs to be verified and at what level of detail, and then to abstract areas of the design which are known to increase complexity and run-time.
The simplest form of abstraction is to remove or exclude a module or function in the design. This works well when a function or part of the design does not affect the functionality to be verified. Another form of abstraction is to replace part of the design with a less complex version that may have less, but still adequate functionality.
Abstraction can be done manually by creating a model to replace part of the design, or automatically by the formal verification tool. Such tools can, for example, easily recognize and remove multipliers or memories.
Abstraction of counters
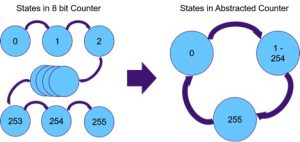
Counters add complexity and sequential depth to a design, but can be easily abstracted. Counters often count to a value and when it is reached, enable or check another function e.g. a bus time-out timer. If a transaction on a bus is not completed before the timer reaches its maximum value, an error is flagged. If the counter is eight bits wide, it takes 256 cycles before the time-out logic can be verified. This sequential depth often causes long run-times. However, the functionality of the time-out logic doesn’t depend on how many cycles the counter is counting, just that it reaches its maximum value. This means that there are only three interesting states for the counter:
- Initial state, 0
- Intermediate values between 1 – 254
- Max value, 255
We can abstract the counter with the 3-state finite state machine (FSM) shown below, instead of a 256 state FSM as in the original counter. Formal verification tools can do this type of abstraction automatically by analyzing which counter values are used in the design.
Figure 1 Speeding 8bit counter verification by abstraction to fewer states (Source: Synopsys)
Abstraction of memories
Memories also increase the complexity of formal verification, but if the behavior of the design that is being verified does not depend on values stored in a particular memory block it can be removed. For example, if the design being verified is a memory controller and a two-port memory and the requirement is to verify that: “the two ports can never be read or written with the same address”, then you don’t need to model the memory since the values stored in it aren’t involved in proving or disproving the property. If the memory is excluded, its outputs may change randomly at any time, which may lead to incorrect behavior. In this case the memory abstraction should be refined to match reality more closely, for example by specifying that read data must not change when the address is not changing. This can be done by an SVA assumption:
stbl: assume property (@(posedge clk) $stable(addr) |-> $stable(data_out));
In other cases, a verification result may depend on data values stored in memory, so it is not possible to exclude the memory. However, you can write an abstracted model of the memory e.g as a cache memory that holds a few of the latest write transactions, or just model a few randomly selected addresses and add constraints to ensure that only these addresses are used. The complexity of the abstracted model will be much less than of the entire memory and so run-times should be shorter.
Abstracting data values
Another powerful abstraction technique is to use symbolic variables for data values. Symbolic variables can take any possible value and keep it stable throughout the verification run.
symb: assume property (@(posedge clk) $stable(symbolic_var));
This can be used, for example, to verify that data is not corrupted when passing through a FIFO.
Figure 2 Speeding the verification of FIFOs by using symbolic variables (Source: Synopsys)
To verify that data is passing through the FIFO correctly, many different values would have to be assigned to data_in and observed on data_out to ensure that no bits are swapped or stuck at zero or one. Instead, by assigning data_in to a symbolic variable when push is asserted and comparing data_out to the symbolic variable when pop is asserted, the complexity and run-time reduced, and the FIFO is verified for every possible value of data_in.
Conclusion
Successful FPV of large designs and SoCs relies on abstractions, and many properties can be proven using tool features such as blackboxing and automatic counter abstractions. If you are using FPV, applying abstractions will enable you to verify more properties in less time and so produce better designs.
